What concepts or facts do you know from math that is mind blowing, awesome, or simply fascinating?
Here are some I would like to share:
- Gödel’s incompleteness theorems: There are some problems in math so difficult that it can never be solved no matter how much time you put into it.
- Halting problem: It is impossible to write a program that can figure out whether or not any input program loops forever or finishes running. (Undecidablity)
The Busy Beaver function
Now this is the mind blowing one. What is the largest non-infinite number you know? Graham’s Number? TREE(3)? TREE(TREE(3))? This one will beat it easily.
- The Busy Beaver function produces the fastest growing number that is theoretically possible. These numbers are so large we don’t even know if you can compute the function to get the value even with an infinitely powerful PC.
- In fact, just the mere act of being able to compute the value would mean solving the hardest problems in mathematics.
- Σ(1) = 1
- Σ(4) = 13
- Σ(6) > 101010101010101010101010101010 (10s are stacked on each other)
- Σ(17) > Graham’s Number
- Σ(27) If you can compute this function the Goldbach conjecture is false.
- Σ(744) If you can compute this function the Riemann hypothesis is false.
Sources:
- YouTube - The Busy Beaver function by Mutual Information
- YouTube - Gödel’s incompleteness Theorem by Veritasium
- YouTube - Halting Problem by Computerphile
- YouTube - Graham’s Number by Numberphile
- YouTube - TREE(3) by Numberphile
- Wikipedia - Gödel’s incompleteness theorems
- Wikipedia - Halting Problem
- Wikipedia - Busy Beaver
- Wikipedia - Riemann hypothesis
- Wikipedia - Goldbach’s conjecture
- Wikipedia - Millennium Prize Problems - $1,000,000 Reward for a solution
There are more ways to arrange a deck of 52 cards than there are atoms on Earth.
I feel this one is quite well known, but it’s still pretty cool.
An extension of that is that every time you shuffle a deck of cards there’s a high probability that that particular arrangement has never been seen in the history of mankind.
With the caveat that it’s not the first shuffle of a new deck. Since card decks come out of the factory in the same order, the probability that the first shuffle will result in an order that has been seen before is a little higher than on a deck that has already been shuffled.
For the uninitiated, the monty Hall problem is a good one.
Start with 3 closed doors, and an announcer who knows what’s behind each. The announcer says that behind 2 of the doors is a goat, and behind the third door is
a carstudent debt relief, but doesn’t tell you which door leads to which. They then let you pick a door, and you will get what’s behind the door. Before you open it, they open a different door than your choice and reveal a goat. Then the announcer says you are allowed to change your choice.So should you switch?
The answer turns out to be yes. 2/3rds of the time you are better off switching. But even famous mathematicians didn’t believe it at first.
I know the problem is easier to visualize if you increase the number of doors. Let’s say you start with 1000 doors, you choose one and the announcer opens 998 other doors with goats. In this way is evident you should switch because unless you were incredibly lucky to pick up the initial door with the prize between 1000, the other door will have it.
I now recall there was a numberphile with exactly that visualisation! It’s a clever visual
How do we even come up with such amazing problems right ? It’s fascinating.
It’s a good one.
It took me a while to wrap my head around this, but here’s how I finally got it:
There are three doors and one prize, so the odds of the prize being behind any particular door are 1/3. So let’s say you choose door #1. There’s a 1/3 chance that the prize is behind door #1 and, therefore, a 2/3 chance that the prize is behind either door #2 OR door #3.
Now here’s the catch. Monty opens door #2 and reveals that it does not contain the prize. The odds are the same as before – a 1/3 chance that the prize is behind door #1, and a 2/3 chance that the prize is behind either door #2 or door #3 – but now you know definitively that the prize isn’t behind door #2, so you can rule it out. Therefore, there’s a 1/3 chance that the prize is behind door #1, and a 2/3 chance that the prize is behind door #3. So you’ll be twice as likely to win the prize if you switch your choice from door #1 to door #3.
deleted by creator
The four-color theorem is pretty cool.
You can take any map of anything and color it in using only four colors so that no adjacent “countries” are the same color. Often it can be done with three!
Maybe not the most mind blowing but it’s neat.
Thanks for the comment! It is cool and also pretty aesthetically pleasing!
Your map made me think how interesting US would be if there were 4 major political parties. Maybe no one will win the presidential election 🤔
What about a hypothetical country that is shaped like a donut, and the hole is filled with four small countries? One of the countries must have the color of one of its neighbors, no?
I think the four small countries inside would each only have 2 neighbours. So you could take 2 that are diagonal and make them the same colour.
Looks to be that way one of the examples given on the wiki page. It is still however an interesting theory, if four countries touching at a corner, are the diagonal countries neighbouring each other or not. It honestly feels like a question that will start a war somewhere at sometime, probably already has.
But each small country has three neighbors! Two small ones, and always the big donut country. I attached a picture to my previous comment to make it more clear.
In your example the blue country could be yellow and that leaves the other yellow to be blue. Now no identical colors touch.
You still have two red countries touching each other, what are you talking about?
Oops I meant the red one goes blue.
Whoops I should’ve been clearer I meant two neighbours within the donut. So the inside ones could be 2 or 3 colours and then the donut is one of the other 2 or the 1 remaining colour.
You’re right. Bad example from my side. But imagine this scenario:
That map is actually still quite similar to the earlier example where all 4 donut hole countries are the same. Once again on the right is the adjacency graph for the countries where I’ve also used a dashed line to show the only difference in adjacency.
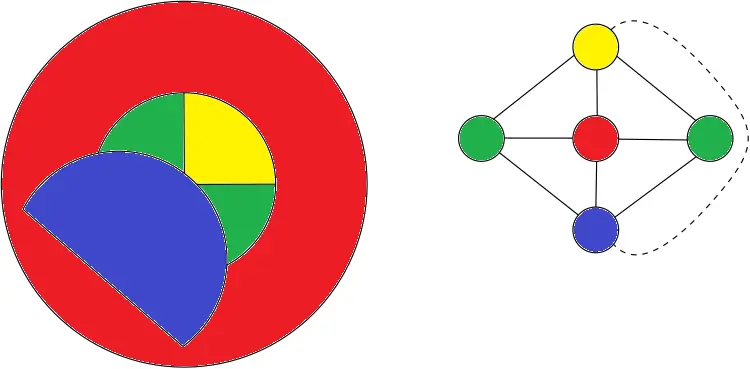
Oh wow, now I feel dumb. Thanks.
Make purple yellow and one of the reds purple.
…There is no purple though?
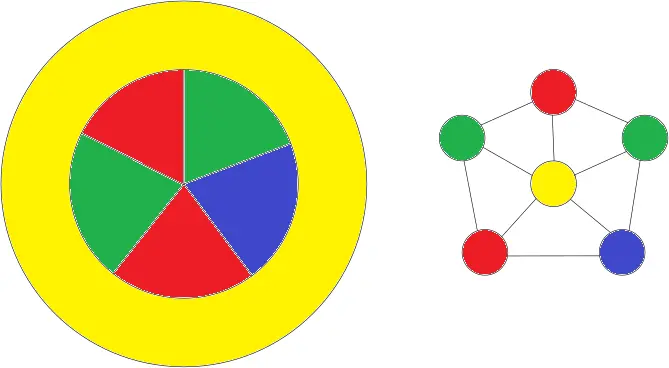
Ok now do this one. What color is the donut country?Someone beat me to it, so I thought I’d also include the adjacency graph for the countries, it can be easier to see the solution to colouring them.
There are some rules about the kind of map this applies to. One of them is “no countries inside other countries.”
Not true, see @BitSound’s comment.
It does have to be topologically planar (may not be the technical term), though. No donut worlds.
The regions need to be contiguous and intersect at a nontrivial boundary curve. This type of map can be identified uniquely with a planar graph by placing a vertex inside each region and drawing an edge from one point to another in each adjacent region through the bounding curve.
I see.
In that image, you could color yellow into purple since it’s not touching purple. Then, you could color the red inner piece to yellow, and have no red in the inner pieces.
Note you’ll need the regions to be connected (or allow yourself to color things differently if they are the same ‘country’ but disconnected). I forget if this causes problems for any world map.
I suspect that the Belgium-Netherlands border defies any mathematical description.
I read an interesting book about that once, will need to see if I can find the name of it.
EDIT - well, that was easier than expected!
Read the author as Robin Williams
deleted by creator
Isn’t the proof of this theorem like millions of pages long or something (proof done by a computer ) ? I mean how can you even be sure that it is correct ? There might be some error somewhere.
Goldbach’s Conjecture: Every even natural number > 2 is a sum of 2 prime numbers. Eg: 8=5+3, 20=13+7.
https://en.m.wikipedia.org/wiki/Goldbach’s_conjecture
Such a simple construct right? Notice the word “conjecture”. The above has been verified till 4x10^18 numbers BUT no one has been able to prove it mathematically till date! It’s one of the best known unsolved problems in mathematics.
How can you prove something in math when numbers are infinite? That number you gave if it works up to there we can call it proven no? I’m not sure I understand
There are many structures of proof. A simple one might be to prove a statement is true for all cases, by simply examining each case and demonstrating it, but as you point out this won’t be useful for proving statements about infinite cases.
Instead you could assume, for the sake of argument, that the statement is false, and show how this leads to a logical inconsistency, which is called proof by contradiction. For example, Georg Cantor used a proof by contradiction to demonstrate that the set of Natural Numbers (1,2,3,4…) are smaller than the set of Real Numbers (which includes the Naturals and all decimal numbers like pi and 69.6969696969…), and so there exist different “sizes” of infinity!
For a method explicitly concerned with proofs about infinite numbers of things, you can try Proof by Mathematical Induction. It’s a bit tricky to describe…
- First demonstrate that a statement is true in some 1st base case.
- Then demonstrate that if it holds true for the abstract Nth case, then it necessarily holds true for the (N+1)th case (by doing some clever rearranging of algebra terms or something)
- Therefore since it holds true for the 1th case, it must hold true for the (1+1)th case = the 2th case. And since it holds true for the 2th case it must hold true for the (2+1)=3th case. And so on ad infinitum.
Wikipedia says:
Mathematical induction can be informally illustrated by reference to the sequential effect of falling dominoes.
Bear in mind, in formal terms a “proof” is simply a list of true statements, that begin with axioms (which are true by default) and rules of inference that show how each line is derived from the line above.
Very cool and fascinating world of mathematics!
As you said, we have infinite numbers so the fact that something works till 4x10^18 doesn’t prove that it will work for all numbers. It will take only one counterexample to disprove this conjecture, even if it is found at 10^100. Because then we wouldn’t be able to say that “all” even numbers > 2 are a sum of 2 prime numbers.
So mathematicians strive for general proofs. You start with something like: Let n be any even number > 2. Now using the known axioms of mathematics, you need to prove that for every n, there always exists two prime numbers p,q such that n=p+q.
Would recommend watching the following short and simple video on the Pythagoras theorem, it’d make it perfectly clear how proofs work in mathematics. You know the theorem right? For any right angled triangle, the square of the hypotenuse is equal to the sum of squares of both the sides. Now we can verify this for billions of different right angled triangles but it wouldn’t make it a theorem. It is a theorem because we have proved it mathematically for the general case using other known axioms of mathematics.
I came here to find some cool, mind-blowing facts about math and have instead confirmed that I’m not smart enough to have my mind blown. I am familiar with some of the words used by others in this thread, but not enough of them to understand, lol.
Please feel free to ask any questions! Math is a wonderful field full of beauty but unfortunately almost all education systems fail to show this and instead makes it seem like raw robotic calculations instead of creativity.
Math is best learned visually and with context to more abstract terms. 3Blue1Brown is the best resource in my opinion for this!
Here’s a mindblowing fact for you along with a video from 3Blue1Brown. Imagine you are sliding a 1,000,000 kg box and slamming it into a 1 kg box on an ice surface with no friction. The 1 kg box hits a wall and bounces back to hit the 1,000,000 kg box again.
The number of bounces that appear is the digits of Pi. Crazy right? Why would pi appear here? If you want to learn more here’s a video from the best math teacher in the world.
Thanks! I appreciate the response. I’ve seen some videos on 3blue1brown and I’ve really enjoyed them. I think if I were to go back and fill in all the blank spots in my math experience/education I would enjoy math quite a bit.
I don’t know why it appears here or why I feel this way, but picturing the box bouncing off the wall and back, losing energy, feels intuitively round to me.
The utility of Laplace transforms in regards to differential systems.
In engineering school you learn to analyze passive DC circuits early on using not much more than ohms law and Thevenin’s Theoram. This shit can be taught to elementary schoolers.
Then a little while later, you learn how to do non-finear differential equations to help work complex systems, whether it’s electrical, mechanical, thermal, hydrolic, etc. This shit is no walk in the park.
Then Laplace transforms/identities come along and let you turn non-linear problems in time-based space, into much simpler problems in frequency-based space. Shit blows your mind.
THEN a mafacka comes along and teaches you that these tools can be used to turn complex differential system problems (electrical, mechanical, thermal, hydrolic, etc) into simple DC circuits you can analyze/solve in frequency-based space, then convert back into time-based space for the answers.
I know this is super applied calculus shit, but I always love that sweet spot where all the high-concept math finally hits the pavement.
And then they tell you that the fundamental equations for thermal, fluid, electrical and mechanical are all basically the same when you are looking at the whole Laplace thing. It’s all the same…
ABSOLUTELY. I just recently capped off the Diff Eq, Signals, and Controls courses for my undergrad, and truly by the end you feel like a fucking wizard. It’s crazy how much problem-solving/system modeling power there is in such a (relatively) simple, easy to apply, and beautifully elegant mathematical tool.
e^(pi i) = -1
like, what?
3Blue 1Brown actually explains that one in a way that makes it seem less coincidental and black magic. Totally worth a watch
If you think of complex numbers in their polar form, everything is much simpler. If you know basic calculus, it can be intuitive.
Instead of z = + iy, write z = (r, t) where r is the distance from the origin and t is the angle from the positive x-axis. Now addition is trickier to write, but multiplication is simple: (a,b) * (c,d) = (ab, b + d). That is, the lengths multiply and the angles add. Multiplication by a number (1, t) simply adds t to the angle. That is, multiplying a point by (1, t) is the same as rotating it counterclockwise about the origin by an angle t.
The function f(t) = (1, t) then parameterizes a circular motion with a constant radial velocity t. The tangential velocity of a circular motion is perpendicular to the current position, and so the derivative of our function is a constant 90 degree multiple of itself. In radians, that means f’(t) = (1, pi/2)f(t). And now we have one of the simplest differential equations whose solution can only be f(t) = k * e^(t* (1, pi/2)) = ke^(it) for some k. Given f(0) = 1, we have k = 1.
All that said, we now know that f(t) = e^(it) is a circular motion passing through f(0) = 1 with a rate of 1 radian per unit time, and e^(i pi) is halfway through a full rotation, which is -1.
If you don’t know calculus, then consider the relationship between exponentiation and multiplication. We learn that when you take an interest rate of a fixed annual percent r and compound it n times a year, as you compound more and more frequently (i.e. as n gets larger and larger), the formula turns from multiplication (P(1+r/n)^(nt)) to exponentiation (Pe^(rt)). Thus, exponentiation is like a continuous series of tiny multiplications. Since, geometrically speaking, multiplying by a complex number (z, z^(2), z^(3), …) causes us to rotate by a fixed amount each time, then complex exponentiation by a continuous real variable (z^t for t in [0,1]) causes us to rotate continuously over time. Now the precise nature of the numbers e and pi here might not be apparent, but that is the intuition behind why I say e^(it) draws a circular motion, and hopefully it’s believable that e^(i pi) = -1.
All explanations will tend to have an algebraic component (the exponential and the number e arise from an algebraic relationship in a fundamental geometric equation) and a geometric component (the number pi and its relationship to circles). The previous explanations are somewhat more geometric in nature. Here is a more algebraic one.
The real-valued function e^(x) arises naturally in many contexts. It’s natural to wonder if it can be extended to the complex plane, and how. To tackle this, we can fall back on a tool we often use to calculate values of smooth functions, which is the Taylor series. Knowing that the derivative of e^(x) is itself immediately tells us that e^(x) = 1 + x + x^(2)/2! + x^(3)/3! + …, and now can simply plug in a complex value for x and see what happens (although we don’t yet know if the result is even well-defined.)
Let x = iy be a purely imaginary number, where y is a real number. Then substitution gives e^x = e^(iy) = 1 + iy + i(2)y(2)/2! + i(3)y(3)/3! + …, and of course since i^(2) = -1, this can be simplified:
e^(iy) = 1 + iy - y^(2)/2! - iy^(3)/3! + y^(4)/4! + iy^(5)/5! - y^(6)/6! + …
So we’re alternating between real/imaginary and positive/negative. Let’s factor it into a real and imaginary component: e^(iy) = a + bi, where
a = 1 - y^(2)/2! + y^(4)/4! - y^(6)/6! + …
b = y - y^(3)/3! + y^(5)/5! - y^(7)/7! + …
And here’s the kicker: from our prolific experience with calculus of the real numbers, we instantly recognize these as the Taylor series a = cos(y) and b = sin(y), and thus conclude that if anything, e^(iy) = a + bi = cos(y) + i sin(y). Finally, we have e^(i pi) = cos(pi) + i sin(pi) = -1.
For me, personally, it’s the divisible-by-three check. You know, the little shortcut you can do where you add up the individual digits of a number and if the resulting sum is divisible by three, then so is the original number.
That, to me, is black magic fuckery. Much like everything else in this thread I have no idea how it works, but unlike everything else in this thread it’s actually a handy trick that I use semifrequently
That one’s actually really easy to prove numerically.
Not going to type out a full proof here, but here’s an example.
Let’s look at a two digit number for simplicity. You can write any two digit number as 10*a+b, where a and b are the first and second digits respectively.
E.g. 72 is 10 * 7 + 2. And 10 is just 9+1, so in this case it becomes 72=(9 * 7)+7+2
We know 9 * 7 is divisible by 3 as it’s just 3 * 3 * 7. Then if the number we add on (7 and 2) also sum to a multiple of 3, then we know the entire number is a multiple of 3.
You can then extend that to larger numbers as 100 is 99+1 and 99 is divisible by 3, and so on.
Waaaait a second.
Does that hold for every base, where the divisor is 1 less than the base?
Specifically hexidecimal - could it be that 5 and 3 have the same “sum digits, get divisibility” property, since 15 (=3*5) is one less than the base number 16?
Like 2D16 is16*2+13 = 45, which is divisible by 3 and 5.
Can I make this into a party trick?! “Give me a number in hexidecimal, and I’ll tell you if it’s divisible by 10.”
Am thinking it’s 2 steps:
- Does it end with a 0, 2, 4, 6, 8, A, C, E? Yes means divisible by 2.
- Do the digits add up to a multiple of 5 (ok to subtract 5 liberally while adding)? Skip A and F. For B add 1; C->2, D->3, E->4. If the sum is divisible by 5, then original number is too.
So if 1 and 2 are “yes”, it’s divisible by 10.
E.g.
- DEADBAE16 (=23349547010): (1) ends with E, ok. (2) 3+4+3+1+4=15, divisible by 5. Both are true so yes, divisible by 10.
- C4744416 (=1287482010): (1) ends with 4, ok. (2) 2+4+7+4+4+4=25, ok.
- BEEFFACE16 (=3203398350): (1) E, ok. (2) 1+4+4+2+4=15, ok.
Is this actually true? Have I found a new party trick for myself? How would I even know if this is correct?
All numbers are dividible by 3. Just saying.
Multiply 9 times any number and it always “reduces” back down to 9 (add up the individual numbers in the result)
For example: 9 x 872 = 7848, so you take 7848 and split it into 7 + 8 + 4 + 8 = 27, then do it again 2 + 7 = 9 and we’re back to 9
It can be a huge number and it still works:
9 x 987345734 = 8886111606
8+8+8+6+1+1+1+6+0+6 = 45
4+5 = 9
Also here’s a cool video about some more mind blowing math facts
I suspect this holds true to any base x numbering where you take the highest valued digit and multiply it by any number. Try it with base 2 (1), 4 (3), 16 (F) or whatever.
11 X 11 = 121
111 X 111 = 12321
1111 X 1111 = 1234321
11111 X 11111 = 123454321
111111 X 1111111 = 12345654321
You could include 1 x 1 = 1
But thats so cool. Maths is crazy.
Amazing in deed!
Just a small typo in the very last factor
1111111.
Euler’s identity, which elegantly unites some of the most fundamental constants in a single equation:
e^(iπ)+1=0
Euler’s identity is often cited as an example of deep mathematical beauty. Three of the basic arithmetic operations occur exactly once each: addition, multiplication, and exponentiation. The identity also links five fundamental mathematical constants:
- The number 0, the additive identity.
- The number 1, the multiplicative identity.
- The number π (π = 3.1415…), the fundamental circle constant.
- The number e (e = 2.718…), also known as Euler’s number, which occurs widely in mathematical analysis.
- The number i, the imaginary unit of the complex numbers.
Furthermore, the equation is given in the form of an expression set equal to zero, which is common practice in several areas of mathematics.
Stanford University mathematics professor Keith Devlin has said, “like a Shakespearean sonnet that captures the very essence of love, or a painting that brings out the beauty of the human form that is far more than just skin deep, Euler’s equation reaches down into the very depths of existence”. And Paul Nahin, a professor emeritus at the University of New Hampshire, who has written a book dedicated to Euler’s formula and its applications in Fourier analysis, describes Euler’s identity as being “of exquisite beauty”.
Mathematics writer Constance Reid has opined that Euler’s identity is “the most famous formula in all mathematics”. And Benjamin Peirce, a 19th-century American philosopher, mathematician, and professor at Harvard University, after proving Euler’s identity during a lecture, stated that the identity “is absolutely paradoxical; we cannot understand it, and we don’t know what it means, but we have proved it, and therefore we know it must be the truth”.
Seeing mathematics visually.
I am a huge fan of 3blue1brown and his videos are just amazing. My favorite is linear algebra. It was like an out of body experience. All of a sudden the world made so much more sense.
His video about understanding multiple dimensions was what finally made it click for me
Imagine a soccer ball. The most traditional design consists of white hexagons and black pentagons. If you count them, you will find that there are 12 pentagons and 20 hexagons.
Now imagine you tried to cover the entire Earth in the same way, using similar size hexagons and pentagons (hopefully the rules are intuitive). How many pentagons would be there? Intuitively, you would think that the number of both shapes would be similar, just like on the soccer ball. So, there would be a lot of hexagons and a lot of pentagons. But actually, along with many hexagons, you would still have exactly 12 pentagons, not one less, not one more. This comes from the Euler’s formula, and there is a nice sketch of the proof here: .
The Fourier series. Musicians may not know about it, but everything music related, even harmony, boils down to this.
Fourier transformed everything
The square of any prime number >3 is one greater than an exact multiple of 24.
For example, 7² = 49= (2 * 24) + 1
Does this really hold for higher values? It seems like a pretty good way of searching for primes esp when combined with other approaches.
Every prime larger than 3 is either of form 6k+1, or 6k+5; the other four possibilities are either divisible by 2 or by 3 (or by both). Now (6k+1)² − 1 = 6k(6k+2) = 12k(3k+1) and at least one of k and 3k+1 must be even. Also (6k+5)² − 1 = (6k+4)(6k+6) = 12(3k+2)(k+1) and at least one of 3k+2 and k+1 must be even.
